... The Programmer God ...
A simulation universe hypothesis at the Planck scale

if we assign geometrical objects to mass, space and time,
and then link them via a unit number relationship,
we can build a physical universe from mathematical structures.
Could a Programmer God have used this approach?
(the simulation universe hypothesis)
The question as to whether our entire universe is a Matrix-style simulation is, like God, considered to be a philosophical debate, for it is presumed that it cannot be proved (or disproved). However there are anomalies in the physical constants that appear to constitute evidence we are in a simulation (they cannot be explained by a physical universe). Furthermore they suggest coding and this implies a Programmer. From these anomalies we can reverse engineer parts of the Programmer's source code. This text is a discussion of that source code.
Note 1. Readers should note that any candidate for a Programmer-God simulation-universe source code, including the code described here, must satisfy these conditions;
1. It can generate physical structures from mathematical forms.
2. The sum universe is dimensionless (simply data on a celestial hard disk).
3. We must be able to use it to derive the laws of physics (because the source code is the origin of the laws of nature, and the laws of physics are our observations of the laws of nature).
4. The mathematical logic must be unknown to us (the Programmer is a non-human intelligence).
5. The coding should have an 'elegance' commensurate with the Programmer's celestial level of skill.
Note 3.
Articles update
The articles 1 to 4 have been updated (Oct 2025) so that they can be read in sequential order (article 2 follows on from article 1...). Further updates pending.
Note 4.
Podcasts (tab)
Google Gemini AI does podcasts of acceptable quality in english and dubious quality in other languages, Here is an example, i will update as time permits ( as of Oct 2025).
1. English podcast
Note 5.
Constants
Formulas for the physical constants in Maple format. These can be used to confirm the results listed.
Note 6.
Wiki sites
- wiki: Overview of the Programmer God
- wiki: Planck units as geometrical objects
-
wiki: Physical constants (anomalies)
-
wiki: Gravitational and atomic orbitals from particle to particle rotating pairs
-
wiki: Mathematical electron
-
wiki: Relativity as the mathematics of perspective
-
wiki: Planck unit universe (cosmic microwave background)
-
Cite wiki pages
Topics
This page gives only a general overview of the model, for the mathematics refer to the articles, these in turn have been translated onto wiki sites for a more complete description. Links are given below. The eBook is due to be updated. Some tables list time object T=2π, they should read T=π.
What is immediately noticeable is the simplicity and elegance of the geometries the Programmer is using. Mass M = 1, time T = 2π, an electron formula that embeds the electron, even quantization of the atom is via a geometrical trick (using a hyperbolic spiral) ... and in this entire model only 2 physical constants are used (alpha and Omega). This elegance is the characteristic signature of the Programmer's handiwork.
- The simulation hypothesis (introduction)
-
Are we in a simulation?
-
The Programmer God
-
The Planck Scale
-
Planck vs. quantum
-
Summary
-
General notes on the physical constants
- Coding our physical constants.
-
Physical units from Mathematical structures
-
Scalars dimensionless to dimensioned
-
Can we use these objects to communicate with Aliens
-
Mathematical electron the electron that isn't
- Consideration on how the Programmer might also solve ...
-
Time 1. simulation clock-rate, 2. dimensioned time, 3. observer time
-
Gravitational orbitals are atomic orbitals (the alpha spiral)
-
The singularity and the celestial hard disk
-
The little big bang
-
Relativity as the mathematics of perspective
-
Particle half-life from particle geometry
-
The End
Note: This model uses only 2 dimensionless constants (alpha, the fine structure constant and Omega). The electron formula derives from the geometry of these 2 constants, yet it can be used to solve the fundamental physical constants (G, h, c, e, me, kB) to experimental precision. How important is this?
In the words of Prof's J. Barrow and J. Webb, Scientific American 292, 56 - 63 (2005) ...
On the physical constants; 'Some things never change. Physicists call them the {constants of nature}. Such quantities as the velocity of light, c, Newton's constant of gravitation, G, and the mass of the electron, me are assumed to be the same at all places and times in the universe. They form the scaffolding around which theories of physics are erected, and they define the fabric of our universe. Physics has progressed by making ever more accurate measurements of their values. And yet, remarkably, no one has ever successfully predicted or explained any of the constants. Physicists have no idea why they take the special numerical values that they do. In SI units, c is 299,792,458; G is 6.673e-11; and me is 9.10938188e-31 -numbers that follow no discernible pattern. The only thread running through the values is that if many of them were even slightly different, complex atomic structures such as living beings would not be possible. The desire to explain the constants has been one of the driving forces behind efforts to develop a complete unified description of nature, or "theory of everything". Physicists have hoped that such a theory would show that each of the constants of nature could have only one logically possible value. It would reveal an underlying order to the seeming arbitrariness of nature.'

Are we in a simulation?
The simulation hypothesis posits that our reality is an artificial reality, such as generated in a computer simulation. The idea was popularized in the 1999 sci-fi film 'The Matrix'.
The ancestor simulation proposes that an advanced civilization could simulate our universe to the degree that we can observe (as with VR helmets today). This version however presumes a base reality, the physical planet of the original programmers. Conversely, a deep-universe (Programmer God) simulation begins with the big bang and constructs the universe in its entirety, down to the smallest detail (see Planck scale).
As the language of mathematics appears to be the language used by the universe, any simulation model that can construct a physical deep-universe has these constraints;
a: the model must be able to construct physical units (of mass, space, time) from dimensionless mathematical structures from within the simulation (for the simulation itself is simply data on a celestial hard disk and has no physical dimensions).
b: the model cannot use dimensioned constants such as G, h, c, e ... as they are a measure of physical units (see a), and so are emergent properties (generated from within the simulation) and not fundamental (not embedded into the source code itself).
c: the model must be independent of any system of units such as kg, m, s, A ... (see a, b) and of any (artificial) numbering system.
This (the mathematical electron) model describes how the above points can be resolved.
The Programming God
As a deep-universe (see 'the Planck scale') simulation hypothesis model is programmed by an external intelligence (the Programmer God), we cannot presume a priori knowledge regarding the simulation source code, other than from this source code the laws of nature emerge (and from which the laws of physics are derived).
Furthermore, although the source code may use mathematical forms we are familiar with (as it would be the origin of these familiar forms), this code would have been developed by a non-human intelligence, and so we may have to develop new mathematical tools to decipher the underlying logic.
For example, the simulation code described here uses a geometrical base-15, the logic behind this is unknown, neither our physics or our mathematics have any corollary.
By implication therefore, the presence of a 'source code' that fits the above criteria could be considered as our first tangible evidence of an external intelligence (external to the universe).
We must also consider that mathematics may simply be a programming language (as with C or Basic or Java ...), and so therefore not an absolute concept in, and of, itself. Although mathematics is the language of physics, and by extension the universe, it may be amiss to assign to mathematics a greater significance.
The Planck Scale
The science vs. God debate exists primarily because God (the 'external' hand) does not appear in the formulas of physics. There is no E = God.c2 for example, and so science has no practical use for a God. As God has no measurable parameters, God is an untestable hypothesis.
Physics is principally divided into studies of the quantum world and the macro world (of planets and stars). These are separated by 2 successful yet incompatible theories; quantum mechanics and relativity. However there is a deeper world, a theoretical world* that is far below the quantum world, and this is called the Planck world. The quantum scale is to the Planck scale as our planetary scale is to the quantum scale.
It is posited here that in a deep-universe simulation, the (fundamental) mathematical laws of nature would operate at this Planck scale, and so to understand both the quantum world and the macro world, we must first begin with the Planck world. In the Planck world we find discrete units; Planck mass is the unit of mass, Planck time is the unit of time, Planck length is the unit of length ... proposed are geometrical objects for mass M, time T, length L ... and it is submitted that these are the origins of the Planck units.
And so it is at the Planck scale where we may find the 'hand' of the Programmer.
*Physics has no tools that can investigate much below the quantum world (the testable laws of physics mostly end around the quantum level), and so this Planck scale remains a theoretical world.
Planck vs. quantum
It is premised here that the simulation operating system works at the Planck scale, with each increment to the simulation clock-rate adding 1 unit of (Planck) time. This is similar to how we program our digital computers.
initialise parameters
FOR age = 1 TO the-end
{
time = time + 1 (generate 1 time object T)
conduct certain processes
}
NEXT age
In this example, age is the incrementing counter (age = 1, 2 3...), it is also the origin of time (for each increment to age we add 1 dimensioned object T (a unit of Planck time), and so the universe gets older, but the variable age itself is just a dimensionless counter. There is this distinction between the dimensionless variable age (the simulation clock-rate) and dimensioned object T (which we measure using seconds; see Time).
age = 1 is the simulation start (a little big bang)
age = the-end is when the simulation ends
The universe is incrementing in discrete steps; age = 1, 2, 3, .... As particles (and photons) have a frequency, in other words a time component (this means they do not exist at any single unit of time), we could consider them as an (oscillating) event that occurs over time. Time is 1 of the dimensions of particles.
For example, if 1 unit of time (1 increment to age) is a 'frame', then the electron is a 'movie'. It takes about 1023 units of time (increments to age) to make 1 electron (1 frame does not a movie make).
The quantum scale is the scale at which we find our electrons and photons. This also means that we cannot interpret the Planck scale using quantum theories, rather the reverse, we must add a time dimension to Planck scale events to interpret the quantum scale. This is why physics uses probabilities to describe quantum events, if the electron does not exist at any 1 unit of time, then we cannot say where the electron is at any 1 unit of time.
If electrons are events that occur over time (they have a frequency), then we too do not exist at unit time, we too are the sum of many (discrete Planck scale) events averaged over time. I inhabit a human body per second
Gravity is an example (see Gravity), if at the Planck scale there is no solid me or solid planet earth (we are both the observed result of events averaged over time), then there is nothing for a gravity force to act on. Instead, if we replace gravity with particle to particle orbital pairs, which is what atoms do (in Hydrogen an electron orbits a proton), and rotate all these together, and map those rotations over time, we will see satellites orbiting planets and planets orbiting stars. Orbits, like particles, emerge over time. There is no need for a gravitational force as we understand it, and as the orbitals are the same, nor is there a need for an electric force.
Summary
At our macro-level of planets and stars, the dimensions of mass, length, time and charge (amperes), represented by the units kg, m, s and A, are independent of each other (we cannot measure the distance from Tokyo to London using pounds or kilograms or amperes).
The units appear to be distinct (mass cannot be confused with length or time), the independence of these units then becoming an inviolable rule, as every high school science student sitting an exam can attest (the units must always add up!).
Indeed, what characterizes a physical universe as opposed to a simulated universe is the notion that there is a fundamental structure underneath, that in some sense mass is, time is and space is … thus we cannot write kg or s in terms of m.
However, upon examination of the f(x) ratios, we may note that they involve combinations of the units (kg m, s, A) that do not appear at our macro level, and so for us the 'mathematical' universe is not apparent, our 'world' is dominated by the 'physical'. At the quantum level however, we find these ratios, and so there we have both jointly the mathematical (the electron formula fe for example), and the physical, the dimensioned parameters (of wavelength, frequency ...).
The Programmer God -ebook
-
A complete discussion of the model in eBook format (note: 2024 edition uploaded).

the Programmer God (eBook)
Physical units from Mathematical structures
The biggest problem with any mathematical universe approach is constructing a physical reality (the physical dimensions of mass, space and time) from mathematical structures. Our computer games may be able to simulate our physical world, but they are still simulations of a physical reality. The 1999 film The Matrix and the ancestor simulation both still begin with a physical level (a base reality), the planet earth.
In this Programmer God model (based on a mathematical electron), the dimensions of our universe (mass, length, time, charge) are geometrical objects MLTA at the Planck scale, furthermore these objects do not simply represent these units (of mass, length, time, charge), they are these units, for what the Programmer has done is choose objects whereby the assigned function; of mass, length, time ... is built into the geometry of the object itself.
We may also find that these objects are not independent, for example, M exhibits mass-ness in conjunction with L length-ness and T time-ness. This arrangement means that, for example, the length object L can combine with the time object T to form a complex object V which is velocity (V = L/T), while still maintaining the underlying attributes of length and time, and so we can construct a universe Lego-style by combining these simple geometrical objects to form more complex geometrical objects (such as electrons and planets).
This however necessitates that the object for length L be able to interact with the objects for time T and mass M and charge A ..., which infers that there must be some relationship between their respective geometries, and indeed it is the evidence of a unit relationship upon which the credibility of this model depends, for this relationship is incompatible with modern physics.

Physics has a set of parameters used to define the universe; such as the speed of light, the strength of gravity ..., these are often referred to as fundamental constants as they cannot be reduced to more fundamental structures.
The 26th General Conference on Weights and Measures (2019 redefinition of SI base units) assigned exact numerical values to 4 physical constants (h, c, e, kB) independently of each other (and thereby confirming these as fundamental constants), and as they are measured in units (kg, m, s, C, ...) these units must also be independent of each other (i.e.: fundamental units).

However, if these constants are interrelated via this unit number relationship, then they cannot all be fundamental constants, and so science cannot independently assign them numerical values.
Scalars
The numerical value of mass object M = 1, the SI equivalent is Planck mass = 2.18 x10-8 kg. Therefore to convert from M to Planck mass we can use a scalar k = 2.18 x10-8 kg where M*k = Planck mass.
M * k = 1 * 2.18 x10-8 kg = 2.18 x10-8 kg
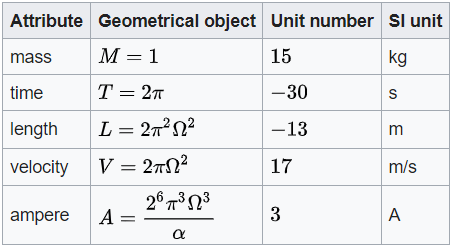
We can assign to each object a scalar; mass k, time t, length l, velocity v, ampere a. The scalars have both the numerical conversion factor (for k = 2.18 x10-8) and the units (for k = kg). The unit number is denoted by θ.

The speed of light c = 299792458 m/s or c = 186200 miles/s ... i.e.: the numerical value of the speed of light depends on the units we use, kilometers or miles.
Likewise, if we were to meet aliens, they would write the speed of light in terms of their units, according to their numbering system, and so the numbering system and units are simply measurement systems, light continues to travel at the same velocity regardless of how we, and the aliens, measure it.
It is proposed that these geometrical MLTVA objects are used by the universe itself, they are built into the simulation source code, and so are 'universal' and independent of any numbering system or units. As example, the reason we can use c = 299792458 m/s or c = 186200 miles/s to measure the speed of light is because embedded within our c is this geometrical object V, which is the real speed of light. Because this V is the geometry of Omega, and Omega has a numerical solution, Omega = 2.007134949, we can assign a numerical value to V = 2πΩ2 = 25.312....
To this V, we then add scalar v;
v = 11843707.905 m/s such that
c = V*v = 299792458 m/s
or scalar v = 7356.08 miles/s such that
c = V*v = 186200 miles/s.
Aliens will also have a value for the speed of light but in alien units, and so their scalar v will not resemble our v (in miles or meters). But for aliens and humans alike, object V will be the same.
The premise is that these MLTVA geometrical objects are used by the universe itself, they are the constructs of mass, space and time. The V term doesn't measure the speed of light, it is that quantity that bestows what we measure as the speed of light, the scalar v is just a conversion factor that we (and aliens) can use. We need a conversion factor because objects such as L or T are too small for daily use, the units that we use, such as seconds or feet or meters, are much more practical than these MLTA units (i.e.: 1 meter, a human size unit, = 6200000000000000000000000000000000 units of this geometrical length L).
If we set our scalar v = 11843707.905m/s then our c = V*11843707.905 = 299792458m/s. If the aliens set their scalar v = @#$/^%, then their c = V*@#$/^%.
If all we are doing is adding scalars then we are achieving little of any practical value, we have just exchanged 1 system of units for another, however, if we could eliminate the scalars, i.e.: if we eliminate scalar v, then for both us and the aliens c = V, and we would now have a common language. To do this, we use this unit number relationship.
* L is a geometrical object, to convert to our unit the meter, first we solve to a numerical value (L = 79.521193...), we are now using the numerical information encoded within these objects, the universe uses geometry, we use numbers. In the process, the geometrical information of L is lost.
** If we must combine mass and length (volume) and time to balance our equations so that the sum universe remains dimensionless (units = 1), then in order for the universe to create time T, the time to read this sentence for example, the universe must concurrently create mass M and space L (the universe has to get bigger and more massive). If time were to reverse, the universe must shrink accordingly.
Speed of light c = object V * scalar v. Planck mass = object M * scalar k ... and so on. If we simply add scalars to each of our MLTA objects then we have achieved nothing of value.
However each scalar is not just a numerical value, but also includes a unit (v has units m/s or miles/s), and so they follow that unit number relationship, i.e.: the scalar v unit number θ = 17, k unit number θ = 15 ...
This then permits us, via this unit relationship, to define each scalar in terms of other scalars, and then we find that we need only 2 scalars to define all the other scalars. For example, the unit number for a = 3, l = -13 and t = -30, and so 3*3 + -13*3 = -30 = t, this then means that if I know the numerical values for scalar a and scalar l then I know the numerical value for scalar t, and if I know t and l then I know the value for k etc.

This then means that we need only 4 numbers (α, Ω and any 2 scalars) to solve our (or the aliens) physical constants. In this table we define scalars k, t, l, a in terms of scalars r and v, and so if we know the numerical values for r and v (α, Ω have fixed values), then we can solve the constants G, h, c, e, me, kB for any chosen set of units, alien or terrestrial (see calculator below).

We can go 1 step further, and find combinations of the constants where the scalars (r, v) cancel. This would then leave us with only the 2 dimensionless constants α and Ω, which means that these combinations are also dimensionless fX structures, and so solving these combinations will return the same numerical values whether we are using terrestrial units or alien units, because of course, sans scalars, we are simply combining the MLTVA object equivalents, without scalars the MLTVA objects are the system of units we, the aliens, and the universe itself, are all using. The electron, a dimensionless combination of MLTA objects, is an example.
This then can be applied as a test of our MLTA objects, if they are in fact the units used by the universe itself then the numerical values will be the same whether we are using our constants, alien constants, or the MLTVA equivalents.
In column 1., I use the values taken from CODATA (the generally accepted values) and in column 2., I solve using MLTVA geometries. As the scalars have cancelled, the values are the same thus confirming the validity of the MLTA objects (in theory column 1 is not equal to column 2, column 1 is column 2). The least precise results are obtained when using the least precise constants; G and kB. Tables taken from the wiki site (physical constant anomalies, link below).

Are these physical constant anomalies evidence we are in a simulation?
wiki: Physical constants (anomalies)
We can use this calculator. The inputs are scalars for the speed of light v and Planck mass k; 2 fundamental units. It then solves the fundamental physical constants based on those 2 scalars. If we input the alien scalars for (v, k), then the calculator will return the alien values for those constants. Hopefully they will be impressed and not zap us.
The electron that isn't
This model is based on the electron formula.
We can use this formula with the (Planck unit) objects for mass M and length L and frequency T to solve the electron mass, wavelength and frequency.

The frequency of the electron is 1023 units of Planck time = feT. The wavelength comprises 1023 units of Planck length = feL. However we have only 1 unit of Planck mass M per fe (1 unit of mass for every 1023 units of time). Let us suppose that the electron is centered on a Planck black hole (this unit of Planck mass). The black-hole electron thesis. For 1023 units of Planck time, this center is obscured by an electric 'cloud' of AL (ampere meters). These AL units then combine with a unit of T and cancel, exposing for 1 unit of Planck time that black hole center.

And so for this 1 unit of time the electron 'has' mass (1 unit of Planck mass). The universe clock ticks and the electric cloud returns. It is this black hole center which gives the electron its point co-ordinates**, the electric state can be considered a wave-state that has no fixed co-ordinates. And so, instead of a physical particle, the electron (as with other particles) is an event that oscillates over time between this magnetic monopole AL electric (wave) state (duration dictated by fe) to a mass (point) state (duration 1 unit of time). Therefore the shorter the particle frequency, the more 'mass-like' the particle properties will appear to have, the longer the frequency, the more 'wave-like'.
This also means that mass is not a constant property of the particle, rather the electron mass that we measure is the frequency of occurrence of these units of Planck mass when averaged over time. We can measure the energy of the electron using the formula E=hf. This h is Planck's constant, and is an energy constant, its value doesnt change, the frequency f term determines how often it occurs (per second), the more often it occurs, the more energy we have.
We can also use E=mc2 and we get the same answer, for some reason hf=mc2. If E=hf measures the frequency of the wave-state, and for every wave-state we have a mass-state (the particle oscillates between the 2 states), and as m refers to mass, then E=mc2 refers to the mass state, and so hf will equal mc2.
The f term measures frequency, but the c term is a constant, and so it is the m term which is the frequency term. In this formula m does not refer to a constant mass, but instead is average mass, it measures the frequency of the mass-state.
Quarks
The charge on the proton is exactly the same magnitude as the charge on the electron, they cancel perfectly, yet the charge on the proton comes from 3 quarks (UUD) and so we might have thought that the electron also gets it charge from quarks.
Curiously, we can solve the electron formula using 3 magnetic monopoles, (AL)*(AL)*(AL). The unit numbers for (AL) = 3 -13 = -10. To continue the quark analogy, our electron would then be DDD = -30 (note: D = -1/3 unit of charge, U = 2/3 unit of charge and time T = -30), the electron as a unit of minus charge (-30);
DDD = (-10 + -10 + -10) = -30
The AL units = -10. A positron (anti-matter electron) has the same charge as a proton, but we don't have a +10 unit number.
However there is 1 more way to solve the electron formula, and that is with AV monopoles (ampere-velocity). The AV has a unit number +20, if we call this our U quark then we can do this
UUD = +20 +20 -10 = +30
Our UUD particle, although otherwise identical to the electron (returns the formula fe), has the same charge as the proton. If protons were formed in the early days (under intense pressure and heat) from positrons, then we would expect the number of protons in the universe to exactly equal the number of electrons. The universe would then be electrically neutral.
If we add a proton UUD and an electron DDD, we get UUDDDD or 2(UDD), the unit numbers 20 -10 -10 = 0, so this entity would be chargeless, similiar to the neutron, which is UDD.
If we combine a U with DDD then 20 -10 -10 -10 = -10 and we get a D, so we can use an electron to swap between U and D quarks. Fun with numbers.
* In standard physics the electron is a subatomic particle ... but it is not clear to physics what a particle is, we find the following definitions;
a particle itself could be a collapsed wave function or a quantum excitation of a field or an irreducible representation of the Poincaré group or a vibrating string or a thing measured in a detector (-wiki).
** In the vision of quantum mechanics (in the formulas physics use), the electron is considered as a point particle with no volume and no size (-google).
*** ChatGPT (AI chatbox):
According to current scientific understanding, the electron is a point-like particle, meaning that it is a very small object that is effectively a point in space and has no size ... While it is possible to imagine such an object in a purely theoretical sense, there is no evidence to suggest that objects without size actually exist in the physical world ... it is possible that the electron could be considered a mathematical particle. This is because, if it is indeed a dimensionless point, then it would have no physical size or shape, and its properties and behavior would be described by mathematical equations rather than physical characteristics.
And so, although the parameters of the electron are well studied, the existence of the actual electron itself cannot be measured, or tested. Science cannot say what the electron itself is, and so it is inferred (by its parameters). For physics, the existence of the electron, like God, is a matter of faith.
Time
There are 3 modes of time.
1) Universe time, the simulation clock-rate. It is a dimensionless incrementing counter, here this variable is labeled age. This foward increment gives us the arrow of time. All particles experience the same age (it is a constant throughout the universe).
initialise parameters
FOR age = 1 TO the-end
conduct certain processes
NEXT age
2) The second. For every increment to the universe clock, a dimensioned object T is generated. This T is analogous to 1 unit of Planck time and so can be measured in seconds. And so the universe clock (that dimensionless incrementing counter age) numerically equates to, but is not the same as, the dimensioned Planck time object T (whose unit is the second). As we are adding 1 Planck time object T per increment to the simulation clock-rate, Planck time is a constant.
initialise parameters
FOR age = 1 TO the-end
create 1 object (time T = π, unit = s)
...
NEXT age
3) Observer time. For the observer, time equates to a change in state, if life was a movie then the incrementing counter age would indicate the number of frames, object time T would represent each physical frame, but we, as actors in this movie, would only be able to detect motion (a change of state). If the Gods pressed the pause button on our movie, our time would stand still, although we could not know this. If for several frames (increments to age) there was no movement (null frames), then we would not register time passing. Only when the frames have different information can we register time. Observer time is relative (see Relativity).
Gravitational and atomic orbitals
According to conventional wisdom, the moon orbits the earth, this is called a gravitational orbit, and it can be calculated precisely. There is a problem however, no one knows what gravity is. Actually there are more problems, how to reconcile with quantum theories ... Of course, as with the electron, physics is also assuming there is a gravity.
I have argued that particles such as electrons are characterized by an (electric) wave-state to (mass) point-state oscillation. One of the dimensions of the electron therefore is time, the electron is an event that occurs over time (this oscillation). And as planets are made of particles, then planets too are events that occur over time.
The particle mass point-state has defined coordinates, the particle wave state not, and so if we could freeze time, to 1 unit of Planck time, then we would not see a solid earth, but instead a series of (mass) points concentrated around a certain region of space (the electric waves might blur our picture). At the next unit of time we will see a different set of points, but also in that defined region of space (our planet earth). This is because, at any unit of Planck time, some particles are in the wave state and some in the mass state, and this keeps changing (as particles oscillate between the 2 states). What we perceive as a solid earth is the averaging over time of all these events that are occurring at the Planck scale.
This means that there is no gravity force between the earth and moon, because at the Planck scale (for any unit of Planck time) there is no earth or moon, just points and waves concentrated around 2 regions of space. At unit (Planck) time, all the particles (in the mass state) in the earth form a link with all the particles (in the mass state) in the moon, and so we have a network of point-to-point (particle-to-particle) pairs which then rotate 1 unit of Planck length (per unit of Planck time). The observed orbit of the earth and moon is the sum of these rotating gravitational particle-to-particle orbital pairs when averaged over time.
The points are particles in the mass state and so gravity is associated with mass. In the atom we use the wave state, however the formulas are the same for atomic orbitals because the orbitals are the same. We have simply exchanged the electric and gravitational forces with wave-wave and point-point rotations. There is no need to reconcile gravity with the quantum for at the Planck scale there is no distinction. The mass point state seldom occurs, most of the time the particle is in the wave-state, and so gravity appears weak accordingly, however actually per unit time, gravity is stronger, it is equivalent to the strong force.
As there is no earth-moon orbit per se, we don't need Newton's gravitational constant G, and we don't have a center of mass so we don't have a barycenter. We just have this n-body universe wide network of particle to particle orbital pairs. If we plot these over time, then we will see moons orbiting planets and planets orbiting suns.
Our world does not exist at Planck time.
Atomic orbitals - the quantum scale
Evidence of the Programmer's handiwork lies in the elegance of the solutions. So far we have concentrated on the Planck scale. In the atom, the electron can occupy only certain energy levels, and these levels have integer values, i.e.: n = 1, 2, 3... and this n is known as the principal quantum number, and from these integer number sets our quantum theories emerge. If we hit an atom with a photon (a light wave), then it can jump between these levels. How it jumps between these levels if it cannot be between these levels is a mystery (i.e.: if the electron can only be in level 1 or level 2 then how does it get from level 1 to level 2?). This is a valid question because the transition process takes time and so there must be an interim state. Actually we have a few more questions, why does the electron orbit the nucleus? what precisely is the 'electric' force? and so on ...
The easiest solution of course is that the electron classically 'travels' from level 1 to level 2, but this defeats the notion of quantization, that the electron can only be in level 1 or level 2. However, the Programmer seems to like simple solutions, so how did He/She solve this one?
A photon moves in a straight line, but if we can trap it between an electron and a proton (a standing wave) then it may rotate around a center point pulling the electron with it, and so we can use trapped photons to make atomic orbitals. This would mean that if we hit the atom with a photon, the photon will collide with the orbital (not difficult, they are both photons), and if the orbital absorbs this photon, then its radius will become longer and the electron will then be orbiting further from the nucleus.
Now for the Programmer's geometrical trick. As the electron moves outwards it is still rotating (the orbital still rotates as it gets longer) and so the electron follows a spiral pattern. The key lies in the spiral, for at certain angles, which correspond to the integer levels, those angles cancel leaving us with those precise integers that we need (r = Bohr radius; 360°=4r, 360+120°=9r, 360+180°=16r, 360+216°=25r ... 720°=∞).
Physicists are happy because they can keep their quantum levels and the rest of us are happy because we can now solve orbitals using our high school math. Kudos to the Programmer.
Mapping the Bohr radius during ionization (starting from n=1), as the H atom electron reaches each n level, it completes 1 orbit (for illustration) then continues outward (actual velocity will become slower as radius increases according to angle β).
By Malcolm Macleod (Platos Cave (physics)) - Own work, CC BY 3.0, Link
A hyperbolic alpha spiral quantises the atom
wiki: Fine structure constant spiral
The singularity and the celestial hard disk
A black-hole has a surface in 3-D space but no physical interior - this is defined as a singularity, it is where the laws of physics break down. This singularity is characterized by mass, a Planck size black-hole would therefore include a unit of Planck mass.
Characters in our computer games are simply 1's and 0's. They may be able to study the physics of their 1's and 0's world (which is the software that defines the game), but they would have no means to study the hard disk upon which their game resides, for that is an electro-magnetic device independent of their data world. A data address on that hard disk would be the interface - the region where their game world ends and the hard-disk begins.
If a particle oscillates between an electric wave-state to Planck mass point state, then the particle has mass. A photon has only the wave-state and so no mass. The photon travels at the speed of light whereas the particle doesn't move (unless pushed). We could then propose that this Planck mass point-state is the center of the particle, around which that wave-state revolves.
And so could this particle Planck mass point-state be a singularity, the interface betwen our worlds, each Planck black hole a single data address on the celestial 'hard disk' upon which our simulation universe resides, the link between our mathematical 'data' simulation world with its laws of physics and the 'electro-magnetic hard disk' world of the Gods?
The little Big Bang
The big bang presumes that the entire universe was concentrated into a single point, time began with the big bang and the universe has been expanding since, but it is still a closed system.
The dimensionless electron formula embeds all the information it needs, that includes the Planck units themselves. Let us suppose there is a dimensionless Planck 'particle' formula fPlanck which also embeds the Planck units, along with any other information as required. Let us further suppose that with each increment to the clock-rate, 1 Planck fPlanck 'particle' is added to our universe. This formula then breaks up and the Planck units emerge (as we find with the electron formula), forming a Planck unit scaffolding to our universe.
initialise parameters
FOR age = 1 TO the-end
add 1 fPlanck 'particle'
{
extract 1 object (time T = π)
extract 1 object (mass M = 1)
extract 1 object (length L = 2π2Ω2)
...
}
...
NEXT age
The universe is about 13.8 billion years old, this equates to 1062 units of Planck time and so age = 1062 (for each increment to age the universe adds 1 object T (1 unit of Planck time).
As mass and length units are also added proportionately, from age we can also calculate the mass and size of the universe (the universe must grow in size and mass accordingly as we are simultaneously introducing objects M and L with every object T and so the universe is not a closed system).
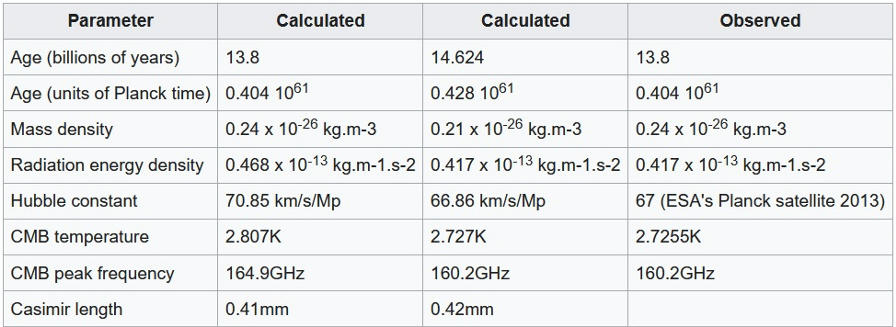
When we calculate the CMB (cosmic microwave background) parameters for a 14.6 billion year old Planck unit universe (we haven't included particles yet), we find it resembles our 13.8 billion year old universe.
The electron particle fe not only embedded the Planck units, it also determined the wavelength and frequency of the electron (as the electron oscillates from point (no size) to wavelength (maximum size in space) back to point. We can draw an analogy with an funiverse 'particle', it will not only include the instruction set for our universe (as fe includes all necessary information for the electron), but will also determine the universe wavelength (maximum size of space) and when the universe will end (frequency).
Relativity as the mathematics of perspective
The mathematics of perspective is a technique used to project a 3-D image onto a 2-D screen (i.e.: a photograph or a landscape painting), using the same approach here would implement a 4-axis expanding (at a constant rate) hyper-sphere super-structure within which 3-D space is a projection.
This expanding hyper-sphere can be used to replace independent particle motion (momentum) with motion as a function of the expansion itself. With each increment to the clock (the variable age), to the universe is added a unit of length L (volume) and a unit of time T, the universe is thereby expanding at the speed of light c for c = 1 unit of Planck length per unit of Planck time (c = lp/tp). As the hypersphere expands, it pulls all particles along with it. This means that all particles and objects (including us) are travelling at, and only at, the speed of this expansion, which is the speed of light (in hyper-sphere co-ordinates). There is only this velocity c. The speed of light then also becomes the limiting speed, for if we could go faster than c we could escape the universe itself.
As photons (the electromagnetic spectrum) have no mass state, they cannot be pulled along by the universe expansion (consequently they are date stamped, as it takes 8 minutes for a photon to travel from the sun, that photon is 8 minutes old when it reaches us), and so photons would be restricted to a lateral motion within the hyper-sphere.
As the electromagnetic spectrum is our principal source of information regarding the environment, we have no direct means to determine this hypersphere expansion, instead we can observe only the objects around us, as if sitting in a plane with the windows closed. And so via the electromagnetic spectrum, a 3-D relative space would be observed (as a projected image from within the 4-axis hyper-sphere), our relativity formulas are translating between the (expanding at the speed of light) hyper-sphere co-ordinates and our observed (relative to each other) 3-D space co-ordinates.
The geometry of particle half-life
Can particle half-life be explained by the particle geometry?
The End
When we calculate the temperature of the universe, we find that it reaches absolute zero (it cannot become colder) when age = 10123, and so the universe cannot grow larger or older. By this time the universe will be uninhabitable, presumably the simulation will be shut down long before this, but the point is that the formula funiverse will include this information as well (if we solve this formula the answer will be 10123, in comparison fe = 1023).
Essentially therefore, we can consider the universe as a particle, with wavelength and frequency, if we can decode this funiverse 'particle' formula, then continuing this analogy, we will anticipate finding embedded within it the electron formula fe along with the information necessary to form protons, neutrons ... and life itself. Furthermore, as it must also be dimensionless, its formula will include the Omega term whereby Ω15*n (where ''n'' is an integer) as this configuration is found in all dimensionless structures. This is because, as noted earlier, the universe uses a geometrical base-15 instead of binary numbers.
wiki: Black-hole_(Planck)
Cite wiki pages
The articles have also been transferred to wik sites, this greatly reduces the text needed. To cite these pages, the versions are given below.
https://en.wikiversity.org/w/index.php?title=God_(programmer)&oldid=2716864
Date of revision: 21 May 2025 01:28 UTC
https://en.wikiversity.org/w/index.php?title=Planck_units_(geometrical)&oldid=2716676
Date of revision: 18 May 2025 07:25 UTC
https://en.wikiversity.org/w/index.php?title=Physical_constant_(anomaly)&oldid=2716670
Date of revision: 18 May 2025 04:33 UTC
https://en.wikiversity.org/w/index.php?title=Quantum_gravity_(Planck)&oldid=2771599
Date of revision: 16 November 2025 01:02 UTC
https://en.wikiversity.org/w/index.php?title=Black-hole_(Planck)&oldid=2771697
Date of revision: 16 November 2025 09:41 UTC
https://en.wikiversity.org/w/index.php?title=Relativity_(Planck)&oldid=2771691
Date of revision: 16 November 2025 09:10 UTC
https://en.wikiversity.org/w/index.php?title=Sqrt_Planck_momentum&oldid=2400924
Date of revision: 17 June 2022 18:55 UTC
https://en.wikiversity.org/w/index.php?title=Electron_(mathematical)&oldid=2771899
Date of revision: 16 November 2025 14:36 UTC
https://en.wikiversity.org/w/index.php?title=Fine-structure_constant_(spiral)&oldid=2706573
Date of revision: 15 March 2025 03:40 UTC
General notes on the physical constants
In the “Trialogue on the number of fundamental physical constants” was debated the number of fundamental dimension units required, noting that "There are two kinds of fundamental constants of Nature: dimensionless alpha and dimensionful (c, h, G). To clarify the discussion I suggest to refer to the former as fundamental parameters and the latter as fundamental (or basic) units. It is necessary and sufficient to have three basic units in order to reproduce in an experimentally meaningful way the dimensions of all physical quantities. Theoretical equations describing the physical world deal with dimensionless quantities and their solutions depend on dimensionless fundamental parameters. But experiments, from which these theories are extracted and by which they could be tested, involve measurements, i.e. comparisons with standard dimensionful scales. Without standard dimensionful units and hence without certain conventions physics is unthinkable".
-Michael J. Duff et al JHEP03(2002)023.
At present, there is no candidate theory of everything that is able to calculate the mass of the electron.
-https://en.wikipedia.org/wiki/Theory-of-everything (02/2016)
Planck units (m_P, l_p, t_p, ampere A_p, T_P) are a set of natural units of measurement defined exclusively in terms of five universal physical constants, in such a manner that these five constants take on the numerical value of G = hbar = c = 1/4pi epsilon_0 = k_B = 1 when expressed in terms of these units. These units are also known as natural units because the origin of their definition comes only from properties of nature and not from any human construct. Max Planck wrote of these units; "we get the possibility to establish units for length, mass, time and temperature which, being independent of specific bodies or substances, retain their meaning for all times and all cultures, even non-terrestrial and non-human ones and could therefore serve as natural units of measurements...".
-Uber irreversible Strahlungsforgange. Ann. d. Phys. (4), (1900) 1, S. 69-122
In 1963, Dirac noted regarding the fundamental constants; "The physics of the future, of course, cannot have the three quantities hbar, e, c all as fundamental quantities, {only two of them can be fundamental, and the third must be derived from those two}."
-Dirac, Paul; The Evolution of the Physicist's Picture of Nature, June 25, 2010
In the article "Surprises in numerical expressions of physical constants", Amir et al write ... In science, as in life, `surprises' can be adequately appreciated only in the presence of a null model, what we expect a priori. In physics, theories sometimes express the values of dimensionless physical constants as combinations of mathematical constants like pi or e. The inverse problem also arises, whereby the measured value of a physical constant admits a `surprisingly' simple approximation in terms of well-known mathematical constants. Can we estimate the probability for this to be a mere coincidence?
-Ariel Amir, Mikhail Lemeshko, Tadashi Tokieda; 26/02/2016, {Surprises in numerical expressions of physical constants}
arXiv:1603.00299 [physics.pop-ph]
"The fundamental constants divide into two categories, units independent and units dependent, because only the constants in the former category have values that are not determined by the human convention of units and so are true fundamental constants in the sense that they are inherent properties of our universe. In comparison, constants in the latter category are not fundamental constants in the sense that their particular values are determined by the human convention of units".
-Leonardo Hsu, Jong-Ping Hsu;
{The physical basis of natural units}; Eur. Phys. J. Plus (2012) 127:11
A charged rotating black hole is a black hole that possesses angular momentum and charge. In particular, it rotates about one of its axes of symmetry. In physics, there is a speculative notion that if there were a black hole with the same mass and charge as an electron, it would share many of the properties of the electron including the magnetic moment and Compton wavelength. This idea is substantiated within a series of papers published by Albert Einstein between 1927 and 1949. In them, he showed that if elementary particles were treated as singularities in spacetime, it was unnecessary to postulate geodesic motion as part of general relativity.
-Burinskii, A. (2005). {"The Dirac–Kerr electron"}. arXiv:hep-th/0507109
The Dirac Kerr–Newman black-hole electron was introduced by Burinskii using geometrical arguments. The Dirac wave function plays the role of an order parameter that signals a broken symmetry and the electron acquires an extended space-time structure. Although speculative, this idea was corroborated by a detailed analysis and calculation.
Mathematical Platonism is a metaphysical view that there are abstract mathematical objects whose existence is independent of us.
-Linnebo, Øystein, {"Platonism in the Philosophy of Mathematics"}, The Stanford Encyclopedia of Philosophy (Summer 2017 Edition), Edward N. Zalta (ed.), plato.stanford.edu/archives/sum2017/entries/platonism-mathematics
Mathematical realism holds that mathematical entities exist independently of the human mind. Thus humans do not invent mathematics, but rather discover it. Triangles, for example, are real entities, not the creations of the human mind.
-https://en.wikipedia.org/wiki/Philosophy-of-mathematics (22, Oct 2017).